Latent Diffusion (Stable Diffusion)

High-Resolution Image Synthesis with Latent Diffusion Models

Takeaways

• This work proposes a method for training diffusion models in a learned latent space (Latent Diffusion Models, LDMs), improving both the training and sampling efficiency of DMs without degrading their quality.
• LDMs learn the encoder/decoder (perceptual compression model) and the DMs separately in two stages such that
  • it doesn’t require a delicate weighting of reconstruction and generative abilities;
  • the same encoder/decoder can be used to train different DMs.
• LDMs incorporate a general-purpose conditioning mechanism based on cross-attention, enabling multi-modal training.
• LDMs achieve new SOTA results for image inpainting and class-conditional image synthesis and highly competitive performance on various tasks, including text-to-image synthesis, unconditional image generation and super-resolution, while significantly reducing computational requirements compared to pixel-based DMs.

Introduction

Image Synthesis

• Autoregressive (AR) transformers (with likelihood-based models)
  • Spectacular results (e.g. DALL-E, VQ-VAE-2).
  • Large models (billions of parameters), high computational cost.
• GANs
  • e.g., BigGAN, StyleGAN.
  • They are mostly confined to data with comparably limited variability.
  • The adversarial learning procedure does not easily scale to modeling complex, multi-modal distributions.
• DMs
  • Learn a hierarchy of denoising autoencoders.
  • Define new SOTA in class-conditional image synthesis (e.g., ADM) and super-resolution (e.g., SR3).
  • Unconditional DMs can readily be applied to tasks such as inpainting and colorization or stroke-based synthesis.
  • Being likelihood-based models, they do not exhibit mode-collapse and training instabilities as GANs.
  • By heavily exploiting parameter sharing, they can model highly complex distributions without involving large AR models.

Problems with DMs

• DMs belong to the class of likelihood-based models, whose mode-covering behavior makes them prone to spend excessive amounts of capacity on modeling imperceptible details of the data
• DMs are computationally demanding, since training and evaluating such a model requires repeated function evaluations (and gradient computations) in the high-dimensional space of RGB images.

Goal: Reducing the computational demands of DMs without impairing their performance.

Semantic Compression and Perceptual Compression

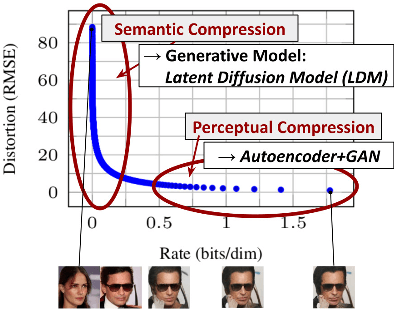
Illustrating perceptual and semantic compression.

Learning a likelihood-based model (e.g., DMs) can be roughly divided into two stages:

1. Perceptual Compression: The model removes high-frequency details but still learns little semantic variation.
2. Semantic Compression: The actual generative model learns the semantic and conceptual composition of the data

The distortion decreases steeply in the low-rate region of the rate-distortion plot, indicating that the majority of the bits are indeed allocated to imperceptible distortion. While DMs allow suppressing this semantically meaningless information by minimizing the responsible loss term, gradients (during training) and the neural network backbone (training and inference) still need to be evaluated on all pixels, leading to superfluous computations and unnecessarily expensive optimization and inference.

Ideas

• Aim to first find a perceptually equivalent, but computationally more suitable space, in which DMs can be trained for high-resolution image synthesis.
• Propose latent diffusion models (LDMs) as an effective generative model and a separate mild compression stage that only eliminates imperceptible details.
• Separate training into two distinct phases:
  1. Train an autoencoder in a lower-dimensional representational space that is perceptually equivalent to the data space.
  2. Train DMs in the learned latent space, which exhibits better scaling properties with respect to the spatial dimensionality.

Advantages:

• The resulting DMs are computationally much more efficient because sampling is performed on a low-dimensional space.
• Exploit the inductive bias of DMs inherited from their UNet architecture, which makes them particularly effective for data with spatial structure and therefore alleviates the need for aggressive, quality-reducing compression levels.
• The general-purpose compression models can be used for training multiple generative models or other downstream applications.

Contributions

• In contrast to purely transformer-based approaches, LDM scales more gracefully to higher dimensional data.
• LDM achieves competitive performance on multiple tasks while significantly lowering computational costs.
• In contrast to previous work that learns both an encoder/decoder architecture and a score-based prior simultaneously, LDM does not require a delicate weighting of reconstruction and generative abilities. This ensures extremely faithful reconstructions and requires very little regularization of the latent space.
• For densely conditioned tasks (e.g., super-resolution, inpainting, and semantic synthesis), LDM can be applied in a convolutional fashion and render large, consistent images.
• A general-purpose conditioning mechanism based on cross-attention is proposed, enabling multi-modal training.

Methods

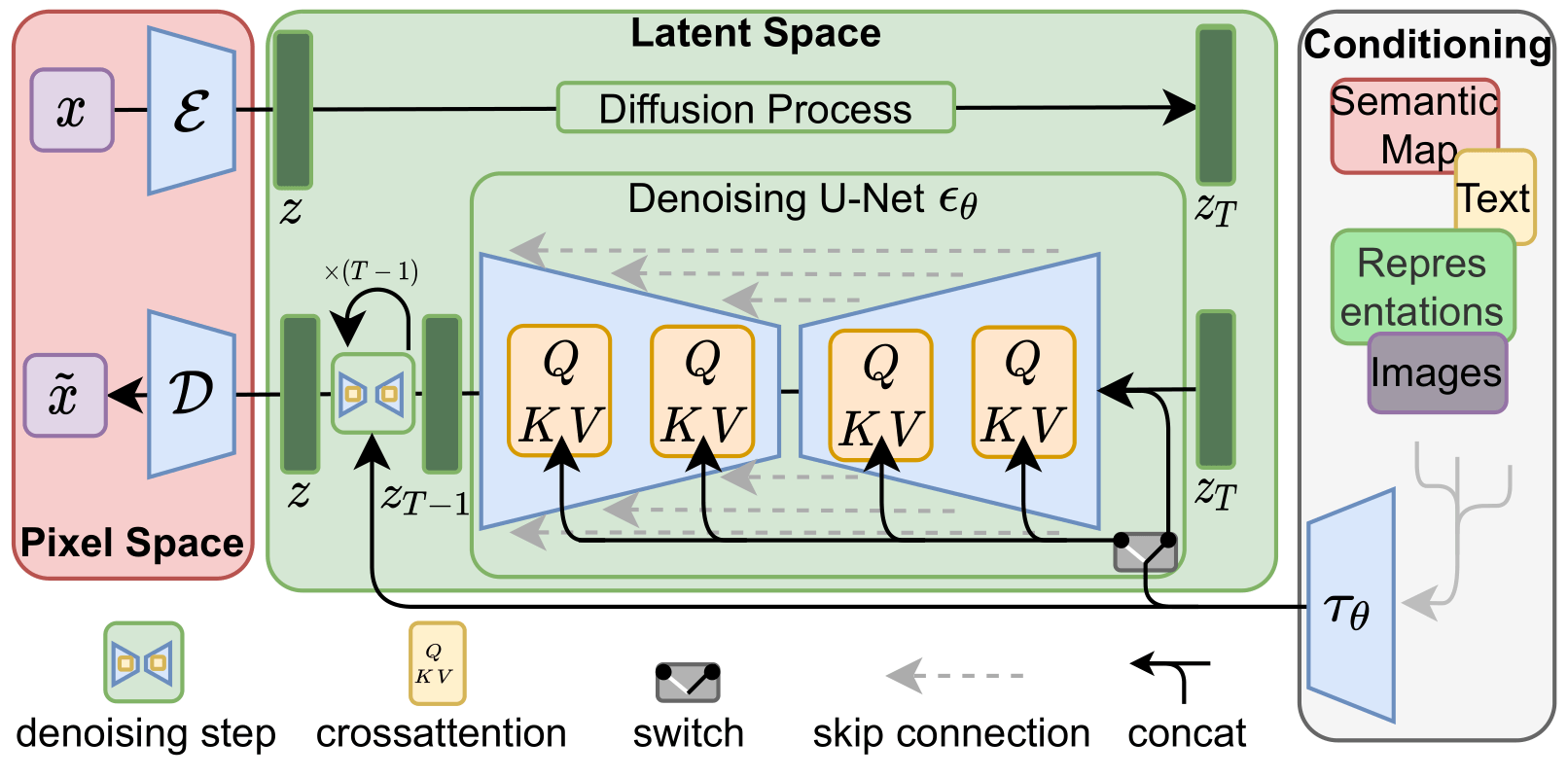
The architecture of LDM.

Perceptual Image Compression (Autoencoder)

The architecture of the perceptual compression model is based on VQGAN.

• An autoencoder architecture

Encoder	Decoder
\(x\in\mathbb{R}^{H\times W\times C}\)	\(z\in\mathbb{R}^{h\times w\times c}\)
\(\text{Conv2D} \rightarrow\mathbb{R}^{H\times W\times C'}\)	\(\text{Conv2D} \rightarrow\mathbb{R}^{H\times W\times C''}\)
\(m\times\{\ \text{ResBlock, Downsample}\}\rightarrow\mathbb{R}^{h\times w\times C''}\)	\(\text{ResBlock}\rightarrow\mathbb{R}^{h\times w\times C''}\)
\(\text{ResBlock}\rightarrow\mathbb{R}^{h\times w\times C''}\)	\(\text{Non-Local Block}\rightarrow\mathbb{R}^{h\times w\times C''}\)
\(\text{Non-Local Block}\rightarrow\mathbb{R}^{h\times w\times C''}\)	\(\text{ResBlock}\rightarrow\mathbb{R}^{h\times w\times C''}\)
\(\text{ResBlock}\rightarrow\mathbb{R}^{h\times w\times C''}\)	\(m\times\{\ \text{ResBlock, Upsample}\}\rightarrow\mathbb{R}^{H\times W\times C'}\)
\(\text{GroupNorm, Swish, Conv2D} \rightarrow\mathbb{R}^{h\times w\times c}\)	\(\text{GroupNorm, Swish, Conv2D} \rightarrow\mathbb{R}^{H\times W\times C}\)

• Loss: a combination of a perceptual loss and a patch-based adversarial objective
• This ensures that the reconstructions are confined to the image manifold by enforcing local realism and avoids blurriness introduced by relying solely on pixel-space losses such as \(L_2\) or \(L_1\) objectives.

1. Given an RGB image \(x\in\mathbb{R}^{H\times W\times 3}\).
2. The encoder \(\mathcal{E}\) encodes \(x\) into a latent representation \(z=\mathcal{E}(x)\in\mathbb{R}^{h\times w\times c}\). The encoder downsamples the image by a factor \(f = H/h = W/w\),
3. The decoder \(\mathcal{D}\) reconstructs the image from the latent, giving \(\tilde{x}=\mathcal{D}(z)=\mathcal{D}(\mathcal{E}(x))\).

To avoid arbitrarily high-variance latent spaces, the authors experiment with two kinds of regularizations.

• KL-reg.
  • KL-penalty towards a standard normal on the learned latent, similar to a VAE.
  • For a KL-regularized latent space, the latent \(z\) is sampled by \(\mathcal{E}(x):=\mathcal{E}_\mu(x)+\mathcal{E}_\sigma(x)\epsilon, \epsilon\sim\mathcal{N}(0,1).\)
  • The latent \(z\) is then rescaled with component-wise variance (i.e., the variance of the entire tensor \(z\)).
• VQ-reg.
  • Use a vector quantization layer within the decoder \(\mathcal{D}\). This model can be interpreted as a VQGAN but with the quantization layer absorbed by the decoder.
  • For a VQ-regularized latent space, features before the quantization layer is extracted as the latent \(z\)
  • No rescaling is needed.

Because the subsequent DM is designed to work with the 2D structure of the learned latent space \(z = \mathcal{E}(x)\), the authors use mild compression rates and achieve very good reconstructions. This is in contrast to previous works (e.g. VQGAN), which relied on an arbitrary 1D ordering of the learned space \(z\) to model its distribution autoregressively and thereby ignored much of the inherent structure of \(z\).

Latent Diffusion Models

Diffusion Models (on Image Domain)

• Probabilistic models designed to learn a data distribution \(p(x)\) by gradually denoising a normally distributed variable.
• Learning the reverse process of a fixed Markov Chain of length \(T\).
• Rely on a reweighted variant of the variational lower bound on \(p(x)\).

• Can be interpreted as an equally weighted sequence of denoising autoencoders \(\epsilon_\theta (x_t, t); t=1,\dots,T\)

  \[L_{DM}=\mathbb{E}_{x,\epsilon\sim\mathcal{N}(0,1),t}\left[ || \epsilon - \epsilon_\theta(x_t,t) ||_2^2 \right]\]

Generative Modeling of Latent Representations

• Use latent space instead of high-dimensional pixel space.
  • Focus on the important, semantic bits of the data.
  • Train in a lower dimensional, computationally much more efficient space.
• Unlike previous work that relied on autoregressive Transformers in a highly compressed, discrete latent space, LDM takes advantage of image-specific inductive biases.
• The neural backbone in LDM \(\epsilon_\theta(\cdot, t)\) is realized as a time-conditional UNet.
  1. The time step \(t\) is mapped to a sinusoidal embedding.
  2. It then goes through Linear, SiLU, Linear, SiLU, Linear
  3. The outputs can be either added to the UNet features or used as affine weights to transform the UNet features.
• Since the forward process is fixed, \(z_t\) can be efficiently obtained from \(\mathcal{E}\) during training.
• Samples from \(p(z)\) can be decoded to image space with a single pass through \(\mathcal{D}\).

• The LDM focuses the objective on the perceptually most relevant bits using the reweighted bound

  \[L_{LDM} = \mathbb{E}_{\mathcal{E}(x),\epsilon\sim\mathcal{N}(0,1),t}\left[ || \epsilon - \epsilon_\theta(z_t,t) ||_2^2 \right].\]

Conditioning Mechanisms

DMs are capable of modeling conditional distributions of the form $$p(z

y)$$.

• This can be implemented with a conditional denoising autoencoder \(\epsilon_\theta(z_t, t, y)\).
• Control the synthesis process through inputs y (e.g., text, semantic maps, or other image-to-image translation tasks).

Augmenting the UNet backbone with the cross-attention mechanism

1. Use a domain-specific encoder \(\tau_\theta(y)\) to project \(y\) to an intermediate representation \(\tau_\theta(y)\in\mathbb{R}^{M\times d_\tau}\).

2. The intermediate (flattened )representation of the UNet \(\varphi_i(z_t)\in\mathbb{R}^{N\times d_\epsilon^i}\) is mapped with a cross-attention layer

   \[\begin{aligned} \text{Attention}(Q, K, V)&=\text{softmax}(QK^T/\sqrt{d})V\\ Q=W_Q^{(i)}\varphi_i(z_t),\quad K&=W_K^{(i)}\tau_\theta(y),\quad V=W_V^{(i)}\tau_\theta(y) \end{aligned}\]

Loss for conditional LDM:

\[L_{LDM} = \mathbb{E}_{\mathcal{E}(x),y,\epsilon\sim\mathcal{N}(0,1),t}\left[ || \epsilon - \epsilon_\theta(z_t,t,\tau_\theta(y)) ||_2^2 \right].\]

Experiments

On Perceptual Compression Tradeoffs

Train class-conditional LDMs on the ImageNet with different downsampling factors \(f\).

• Small downsampling factors for \(f=1,2\) result in slow training progress.
• Overly large values of \(f\) cause stagnating fidelity after comparably few training steps. This might be due to
  • leaving most of the perceptual compression to the diffusion model,
  • too strong first stage compression resulting in information loss and thus limiting the achievable quality.
• LDMs with \(f=4\sim 16\) strike a good balance between efficiency and perceptually faithful results.

Train LDMs on CelebAHQ and ImageNet with different \(f\) and plot sample speed against FID scores.

• LDMs with \(f=4,8\) achieve much lower FID scores while simultaneously significantly increasing sample throughput, compared to pixel-level DMs (\(f=1\)).
• Complex datasets such as ImageNet require reduced compression rates to avoid reducing quality.
• LDMs with \(f=4,8\) offer the best conditions for achieving high-quality synthesis results.

Image Generation with Latent Diffusion

Train unconditional LDMs and evaluate:

• sample quality (FID)
• coverage of the data manifold (Precision and Recall)

Results:

• New SOTA FID on CelebA-HQ.
• Outperform LSGM (a latent diffusion model is trained jointly together with the first stage).
• Outperform prior diffusion-based approaches on all but the LSUN-Bedrooms dataset.
• LDMs consistently improve upon GAN-based methods in Precision and Recall, thus confirming the advantages of their mode-covering likelihood-based training objective over adversarial approaches.

Conditional Latent Diffusion

• Cross-attention and domain-specific encoder \(\tau_\theta\) (Transformers):
  • text-to-image
  • sematic layouts-to-image
• Embedding for each class (added to time embedding)
  • Class-conditional image generation
• Concatenate spatially aligned conditioning information to the input of \(\epsilon_\theta\)
  • image-to-image translation
  • semantic synthesis
  • super-resolution
  • inpainting

Text-to-Image Synthesis

• Train a 1.45B parameter KL-regularized LDM conditioned on language prompts on LAION-400M dataset.
• Use BERT-tokenizer
• Implement \(\tau_\theta\) as a transformer to infer a latent code
• The model generalizes well to complex, user-defined text prompts.

Layouts-to-image Synthesis

• Use a Transformer-based \(\tau_\theta\) similar to the text-to-image synthesis.
• The layout-to-image model discretizes the spatial locations of the bounding boxes and encodes each box as a \((l, b, c)\)-tuple, where \(l\) denotes the (discrete) top-left and \(b\) the bottom-right position. Class information is contained in \(c\).

Semantic Synthesis

• Use images of landscapes paired with semantic maps.
• Concatenate downsampled versions of the semantic maps with the latent image representation of a \(f = 4\) model.
• Train on an input resolution of \(256^2\) (crops from \(384^2\)).
• Generalize to larger resolutions and can generate images up to the megapixel regime when evaluated in a convolutional manner.

Super-Resolution with Latent Diffusion

LDMs can be efficiently trained for super-resolution by directly conditioning on low-resolution images via concatenation.

LDM-SR (trained with bicubic degradation)

• Qualitative and quantitative results show competitive performance of LDM-SR and SR3
  • LDM-SR outperforms SR3 in FID.
  • SR3 has a better IS.
• Results of human preference affirm the good performance of LDM-SR.
• PSNR and SSIM can be pushed by using a post-hoc guiding mechanism (image-based guider)
• LDM-SR does not generalize well to images that do not follow this pre-processing.

LDM-BSR (a generic model trained with more diverse degradation)

• JPEG compressions noise, camera sensor noise, different image interpolations for downsampling, Gaussian blur kernels, and Gaussian noise (applied in random order).
• LDM-BSR produces images much sharper than the models confined to a fixed preprocessing, making it suitable for real-world applications.

Inpainting with Latent Diffusion

Inpainting is the task of filling masked regions of an image with new content either because parts of the image are corrupted or to replace existing but undesired content within the image.

Use the general approach for conditional image generation (concatenation)

The best model:

• A larger diffusion model that has 387M parameters instead of 215M
• Use the VQ-regularized for the first stage and remove attention (non-local layer).
• Fine-tune the model for half at resolution \(512^2\).

Convolutional Sampling

• The LDMs generalize to larger resolutions and can generate images up to the megapixel regime when evaluated in a convolutional manner.
• The authors exploit this behavior in semantic synthesis, super-resolution, and inpainting.

The SNR induced by the variance of the latent space (i.e., \(\text{Var}(z)/\sigma_t^2\)) significantly affects the results for convolutional sampling.

• For the KL-regularized model, this ratio is high, such that the model allocates a lot of semantic detail early on in the reverse denoising process.
• When rescaling the latent space by the component-wise standard deviation of the latents, the SNR is decreased.
• The VQ-regularized space has a variance close to 1, such that it does not have to be rescaled.

Limitations

• While LDMs significantly reduce computational requirements compared to pixel-based approaches, their sequential sampling process is still slower than that of GANs.
• The use of LDMs can be questionable when high precision is required.